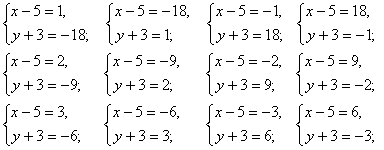Решить уравнение xy + 3x - 5y = -3 в целых числах.

____________________________________________

В данном уравнение левая часть явно на множители не разлагается. Однако, мы можем к обоим частям добавить целые числа, чтобы разложить левую часть на множители:

x(y + 3) - 5y = -3;

x(y + 3) - 5y -15 = -18;

(x - 5)(y + 3) = 18.

Получаем следующие системы:

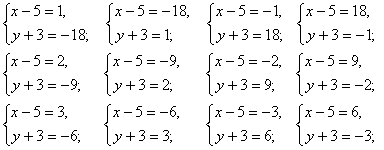
Решая их, получаем следующие ответы (x; y) - (6; -21), (-13; -2), (4; 15), (23; -4), (7; -12), (-4; -1), (3; 6), (14; -5), (8; -9), (-1; 0), (2; 3), (11; -6).

Ответ: пары (x; y) равны (6; -21), (-13; -2), (4; 15), (23; -4), (7; -12), (-4; -1), (3; 6), (14; -5), (8; -9), (-1; 0), (2; 3), (11; -6).

Решить уравнение 4x³ - 2y³ - z³ = 0 в целых числах.

___________________________________________

В данной задаче левая часть не разлагается на множители и, вообще, сложно найти преобразование, ведущее к решению этой задаче.

Остается исследовать свойства чисел, входящие в уравнение. Один из вариантов - метод бесконечного спуска.

В данном уравнении 4x³ и - 2y³ делятся на 2, значить и z³ должно делиться на 2. Обозначим z = 2z₁, где z₁ ∈ Z.

Подставляем в исходное уравнение, получаем:

4x³ - 2y³ - 2³z₁³ = 0;

2x³ - y³ - 4z₁³ = 0.

Теперь мы видим, что 2x³ и - 4z₁³ делятся на 2. Значит и - y³ должно делится на 2. Обозначим y = 2y₁, где y₁ ∈ Z.

Тогда 2x³ - 2³y₁³ - 4z₁³ = 0;

x³ - 4y₁³ - 2z₁³ = 0.

Отчего следует, что x³ делится на 2. Полагая, что x = 2x₁, где x₁ ∈ Z, получим:

2³x₁³ - 4y₁³ - 2z₁³ = 0;

4³x₁³ - 2y₁³ - z₁³ = 0.

Какие выводы можно сделать? Мы видим, что тройка (x; y; z) должна быть четная. Но при этом числа (x₁; y₁; z₁), которые равны предыдущей тройке уменьшенной на 2, также удовлетворяют уравнению. Но раз так, значит и они должны делиться на 2.

Получается, что числа удовлетворяющие условию задачи должны быть четными, сколько бы раз мы их не делили на 2. Единственным четным числом, удовлетворяющим данное условие есть 0. Из чего делаем вывод, что решение данного уравнения одно x = y = z = 0.

Ответ: x = y = z = 0.

Найти остатки от деления квадрата целого числа на 3.

______________________________________________

Целое число x при делении на 3 может давать следующие остатки: 0, 1, 2. Рассмотрим все случаи:

Пусть x = 3k (k ∈ Z).

x² = (3k)² = 9k². Т.е. остаток будет равен 0.

Пусть x = 3k + 1 (k ∈ Z).

x² = (3k + 1)² = 9k² + 6k + 1. Видим, что первые два слагаемые делятся на 3, а третье дает остаток 1, потому и квадрат числа в данном случае будет давать остаток 1 при делении на 3.

Пусть x = 3k + 2 (k ∈ Z).

x² = (3k + 2)² = 9k² + 6k + 4. Видим, что первые два слагаемые делятся на 3, а третье также дает остаток 1, потому и квадрат будет иметь остаток равен 1 при делении на 3.

Мы перебрали все случаи и видим, что квадрат целого числа при делении на 3 всегда дает остаток 0 или 1.

Ответ: Остаток равен 0 или 1.