Доказать, что 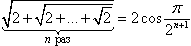 .
.
____________________________________
Воспользуемся методом математической индукции.
1. База индукции.
При k = 1, 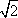 = 2cosπ/4. Утверждение верно.
= 2cosπ/4. Утверждение верно.
2. Переход индукции.
Допустим при неком k = n (n ∈ N) выражение
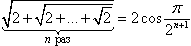
истинно. Докажем, что оно верно и при k = n + 1, т.е.
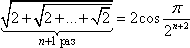
Но так как (исходя из истинности перехода индукции)
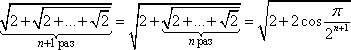
то нам нужно доказать следующее утверждение:
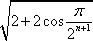 = 2cosπ/2n+2.
= 2cosπ/2n+2.
Делаем преобразования:
2 + 2cosπ/2n+1 = 4cos2 π/2n+2.
Для доказательства этого равенства воспользуемся формулой понижения степени косинуса 2cos2x = cos2x + 1. Тогда
4cos2 π/2n+2 = 2(cosπ/2n+1 + 1) = 2cosπ/2n+1 + 2. Что и требовалось доказать.
Переход доказан, а потому исходное утверждение верно при любом n ∈ N.
Найти все положительные корни уравнения nxn+1 - (n+1)xn + 1 = 0.
_________________________________________________________
Запишем уравнение в следующем виде:
nxn+1 - (n+1)xn + 1 = nxn(x - 1) - (xn - 1) = (x - 1)(nxn - xn-1 - xn-2 - ... - 1) = 0.
Очевидно, что x = 1 - корень уравнения. Докажем, что других положительных корней нет.
Действительно, если x > 1, то xn > xi, где i < n, а потому
nxn - xn-1 - xn-2 - ... - 1 > nxn - nxn-1 > 0.
Если же 0 < x < 1, то xn < xi, где i < n, а потому
nxn - xn-1 - xn-2 - ... - 1 < nxn - nxn-1 < 0.
Что и требовалось доказать.
Ответ: x = 1.
Целые числа x, y, z удовлетворяют уравнению x3 + y3 = z3. Доказать, что хотя бы одно из этих чисел делится на 3.
____________________________________________________________________________
Докажем от обратного. Допустим все три числа x, y, z не делятся на 3. Тогда их можно представить в виде x = 3a ± 1, y = 3b ± 1, z = 3c ± 1. Наше уравнение будет иметь вид:
(3a ± 1)3 + (3b ± 1)3 = (3c ± 1)3;
27a3 ± 27a2 + 9a ± 1 + 27b3 ± 27b2 + 9b ± 1 = 27c3 ± 27c2 + 9c ± 1;
9(3a3 ± 3a2 + a + 3b3 ± 3b2 + b - 3c3  3a2 - c) =
3a2 - c) =  1 ± 1
1 ± 1  1.
1.
Левая часть равенства делится на 9. Правая часть не делится при любов из вариантов знака ±. Мы пришли к противоречию. А значит одно из чисел делится на 3.
Что и требовалось доказать.
Вычислить сумму 1/1·2 + 1/2·3 + ... + 1/n·(n + 1), где n ∈ N.
____________________________________________
Воспользуемся следующим равенством:
1/k - 1/(k + 1) = 1/k·(k + 1).
Тогда нашу сумму можно переписать в следующем виде:
1/1·2 + 1/2·3 + ... + 1/n·(n + 1) = 1/1 - 1/2 + 1/2 - 1/3 + ... + 1/n - 1/(n + 1) = 1 - 1/(n + 1).
Ответ: 1 - 1/(n + 1).
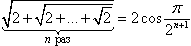 .
. = 2cosπ/4. Утверждение верно.
= 2cosπ/4. Утверждение верно.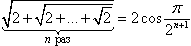
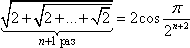
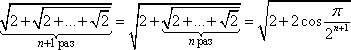
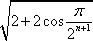 = 2cosπ/2n+2.
= 2cosπ/2n+2.


 3a2 - c) =
3a2 - c) =